統計学の世界では、母集団の性質を直接知ることは困難なため、標本から母集団のパラメータ(平均や分散など)を推定する手法が重要になります。
この記事では、初学者にも理解しやすいように「不偏推定量」について、推定量の基本から具体例まで丁寧に解説していきます。
不偏推定量とは
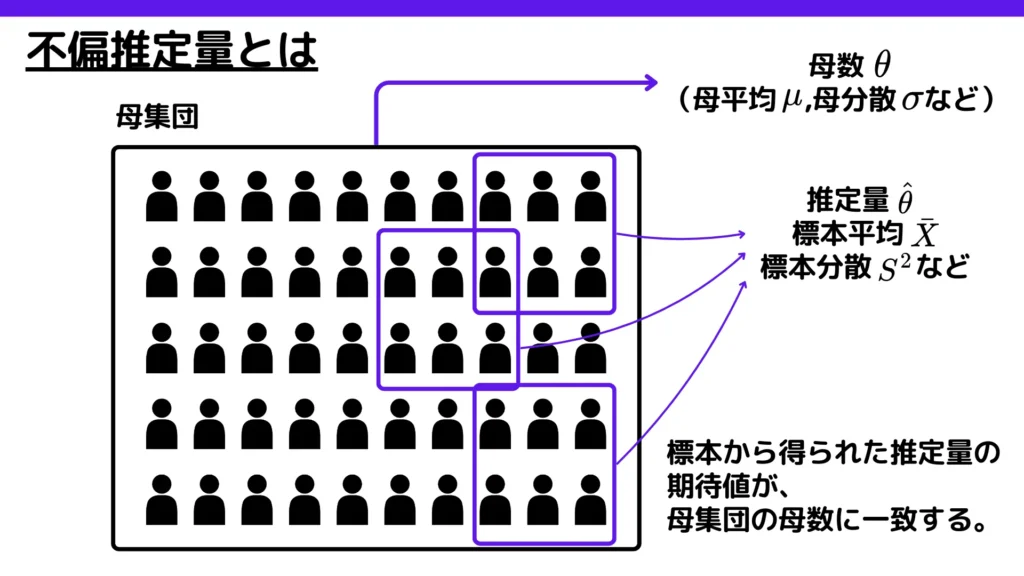
不偏推定量とは、標本から得られた推定量(標本平均など)の期待値が、真の母数と一致する推定量です。
ある推定量が不偏推定量かどうかは、その推定量の期待値を算出することで確かめることができます。
推定量の期待値が真の母数と一致していれば、不偏推定量となります。
そもそも推定量とは?
推定量とは、実際のデータ(標本)から母集団の特徴を推測するための値です。
一般的には母平均\(\mu\)・母分散\(\sigma\)の推定量について取り上げられることが多いです。
例えば、標本\(X_1,X_2,…,X_n\)から得られた標本平均\(\bar{X}\)は母平均\(\mu\)の推定量です。
推定量は実際のデータ(標本)に基づいて計算されるため、標本ごとに毎回異なる値を取ります。
不偏性とは?
標本から得られた推定量の期待値が、真の母数と一致する性質です。
母数を\(\theta\)としたとき、推定量は\(\hat{\theta}\)で表現されることが多いです。
この推定量\(\hat{\theta}\)が不偏性を持つとは、\(\hat{\theta}\)の期待値が母数\(\theta\)と一致することです。これを数式で表現すると、
$$E[\hat{\theta}] = \theta$$
となります。
標本平均は不偏推定量?
最も代表的な推定量と言えば、標本平均\(\bar{X}\)です。
そして、標本平均は不偏推定量であることが知られています。
実際に不偏性が成立しているかどうかを確認してみましょう。
標本平均は以下の式で求められます。
$$\bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i$$
\(\bar{X}\)の期待値を求めると、
$$E[\bar{X}] = E\left[\frac{1}{n}\sum_{i=1}^{n} X_i\right] $$
和の期待値は期待値の和に等しい(期待値の線形性)ので、
$$= \frac{1}{n}\sum_{i=1}^{n} E[X_i] $$
$$= \frac{1}{n}\sum_{i=1}^{n} \mu $$
$$= \frac{n\mu}{n} = \mu$$
標本平均の期待値は真の平均値に一致している、つまり不偏性が成り立っていることが分かります。
標本分散は不偏推定量?
標本分散は不偏推定量ではないことが知られています。
実際に確認してみましょう。
標本分散\(S_n^2\)は以下で求められます。
$$S_n^2 = \frac{1}{n} \sum_{i=1}^{n} \left( X_i – \bar{X} \right)^2$$
欲しい形を求めるために、まずは標本分散の一部(偏差平方和)に対して以下のような変形を行います。
$$\sum_{i=1}^{n} \left( X_i – \bar{X} \right)^2 = \sum_{i=1}^{n} \left[ (X_i – \mu) – (\bar{X} – \mu) \right]^2$$
$$= \sum_{i=1}^{n} \left\{ (X_i – \mu)^2 – 2(X_i – \mu)(\bar{X} – \mu) + (\bar{X} – \mu)^2 \right\}$$
$$= \sum_{i=1}^{n} (X_i – \mu)^2 – 2(\bar{X} – \mu)\sum_{i=1}^{n}(X_i – \mu) + n(\bar{X} – \mu)^2$$
ここで、第二項は\(\sum_{i=1}^{n}(X_i – \mu) = n(\bar{X} – \mu)\) であるから、
$$- 2(\bar{X} – \mu)\sum_{i=1}^{n}(X_i – \mu) = -2n(\bar{X} – \mu)^2$$
先ほどの式に戻ると、
$$\sum_{i=1}^{n} (X_i – \mu)^2 – 2(\bar{X} – \mu)\sum_{i=1}^{n}(X_i – \mu) + n(\bar{X} – \mu)^2= \sum_{i=1}^{n} (X_i – \mu)^2 – n(\bar{X} – \mu)^2$$
ここまでで、
$$\sum_{i=1}^{n} \left( X_i – \bar{X} \right)^2= \sum_{i=1}^{n} (X_i – \mu)^2 – n(\bar{X} – \mu)^2$$
が得られました。
この状態で期待値を求めます。ここまでで求まった式より、
$$E[S_n^2] = E[\frac{1}{n} \sum_{i=1}^{n} \left( X_i – \bar{X} \right)^2]$$
\begin{equation}=E[\frac{1}{n}\sum_{i=1}^{n} (X_i – \mu)^2] – E[(\bar{X} – \mu)^2]\tag{1} \end{equation}
ここで、第一項は母分散で
\begin{equation} \sigma^2=E[(X_i – \mu)^2]\tag{2} \end{equation}
第二項は標本平均の分散で、これは分散の和に分解出来るから、
$$V[\bar{X}]=E[(\bar{X} – \mu)^2]$$
$$V[\bar{X}]=V[\frac{X_1+X_2+…+X_n}{n}]$$
$$=\frac{1}{n^2}V[X_1+X_2+…+X_n]$$
$$=\frac{1}{n^2}n\sigma^2$$
\begin{equation}=\frac{\sigma^2}{n}\tag{3}\end{equation}
(1)に戻って、標本分散の期待値は、
$$E[S_n^2]= E[\frac{1}{n}\sum_{i=1}^{n} (X_i – \mu)^2 – (\bar{X} – \mu)^2]$$
(2),(3)より、
$$ = \sigma^2 – \frac{\sigma^2}{n} = \frac{n-1}{n}\sigma^2$$
このように、何も考えず標本分散の期待値を求めると、母分散とは一致しません。
したがって、正しい母分散の推定には、この補正を行った不偏分散が用いられます。
$$S^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left( X_i – \bar{X} \right)^2$$
この不偏分散の期待値を取ると、真の母分散に一致することが知られています。
$$E[S^2]=\sigma^2$$
標本平均を用いるために自由度が1減少することを補正するため、と解釈することもできます。
ちなみに(3)の分散の計算では、各標本が独立かつ同分布であることを利用しています。
詳しくは以下の記事を参考にしてください!
まとめ
この記事では、統計学の基礎概念である推定量とその不偏性について、解説しました。
標本平均が不偏推定量であり、分散の推定には不偏分散(標本数-1で割る方法)が使われる理由を理解することは、標本や確率分布を扱う上で非常に重要です。
なぜ不偏分散にn-1が現れるのか、不偏性の証明まで理解してから使いましょう!




